最大公約数と関数型プログラミング

配列の全ての要素の最大公約数を求める (Java 8, Python) - Qiita

この記事を見て思いついた。そうだ。最大公約数（greatest common divisor）の話をしよう。

最大公約数を求める

まずは定義から。最大公約数の定義は以下の通り。

2つ以上の正の整数に共通な約数（公約数）のうち最大のもの

折角なので何か例題を立ててみよう。

例題1

20 と 32 の最大公約数を求めよ。

簡単な数だし，まずは暗算で解いてみる。それぞれの値を素因数分解すると以下のようになる。

\begin{align*} 20 &= 2^2 \times 5 \\ 32 &= 2^5 \end{align*}

これにより最大公約数は $2^2 = 4$ だということが分かる。簡単でよかったね。

ユークリッドの互除法

さて，最大公約数を求める機械向けの計算方法としては「ユークリッドの互除法」が有名である。具体的な手順は以下の通り。

32 を 20 で割った余りは 12
20 を 12 で割った余りは 8
12 を 8 で割った余りは 4
8 を 4 で割った余りは 0
したがって 32 と 20 の最大公約数は 4 である

これを図形で表すとこんな感じになる。（以下の図は Wikipedia のものを拝借した。 CC-BY-SA-3.0 で公開されている）

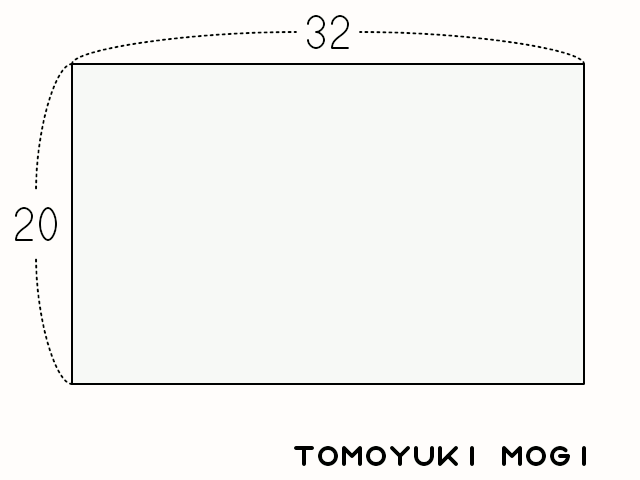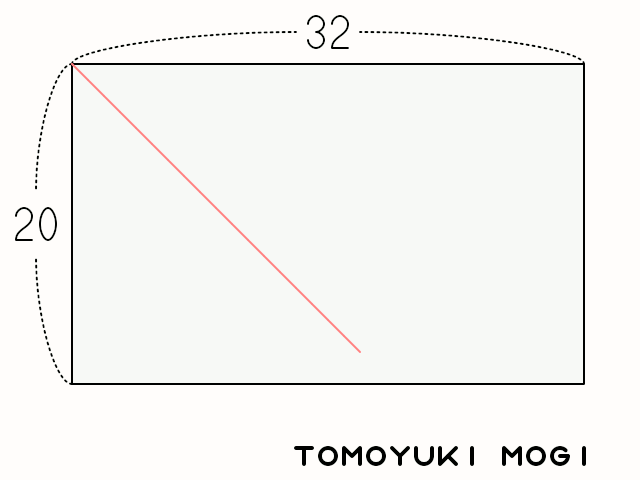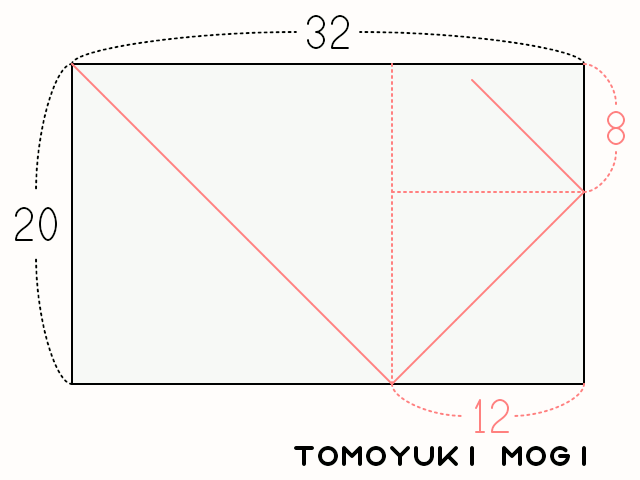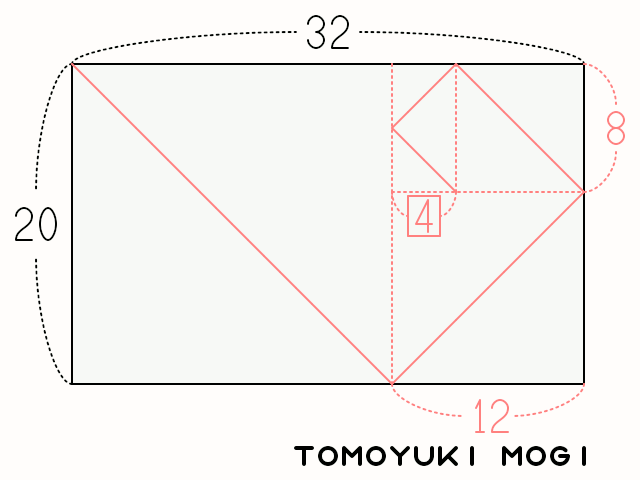
今回はユークリッドの互除法の証明は割愛するとして¹，上記の手順の 1 から 4 は再帰処理になっていることが分かる。というわけで，こんな感じのコードを組んでみる。（だいぶ端折ったコードでゴメン）

package main

import "fmt"

func gcd(a, b int) int {
    if b == 0 {
        return a
    }
    return gcd(b, a%b)
}

func main() {
    fmt.Println(gcd(32, 20)) // 4
}

これで実行結果は 4 になる。

実は Go 言語にも最大公約数を求める関数が標準パッケージ math/big に用意されている。こんな感じで使える。

package main

import (
    "fmt"
    "math/big"
)

func gcd(m, n uint64) uint64 {
    x := new(big.Int)
    y := new(big.Int)
    z := new(big.Int)
    a := new(big.Int).SetUint64(m)
    b := new(big.Int).SetUint64(n)
    return z.GCD(x, y, a, b).Uint64()
}

func main() {
    fmt.Println(gcd(20, 32)) // 4
}

big.Int.GCD() 関数もユークリッドの互除法の一種で，正の整数 $a$, $b$ に対する最大公約数を $\mathrm{gcd}(a, b)$ とすると

\[ \mathrm{gcd}(a, b) = ax + by \]

となる $x$, $y$ の組み合わせを探すものだ。

3つ以上の数の最大公約数

では3つ以上の数の最大公約数を求めるにはどうすればいいか。ちょっと考えれば分かるが，たとえば $a$, $b$, $c$ の最大公約数を求めたいなら $\mathrm{gcd}(\mathrm{gcd}(a, b), c)$ とすればいい。

では例題を立ててみよう。これは「配列の全ての要素の最大公約数を求める」の設問と同等と言える。

例題2

(290021904, 927964716, 826824516, 817140688) の最大公約数を求めよ。

まずはベタに for 文を回してベタに解いてみる。

package main

import (
    "fmt"
    "math/big"
)

func gcd(m, n uint64) uint64 {
    x := new(big.Int)
    y := new(big.Int)
    z := new(big.Int)
    a := new(big.Int).SetUint64(m)
    b := new(big.Int).SetUint64(n)
    return z.GCD(x, y, a, b).Uint64()
}

func main() {
    values := []uint64{290021904, 927964716, 826824516, 817140688}

    z := values[0]
    for _, n := range values {
        z = gcd(n, z)
    }
    fmt.Println(z) // 92
}

ふむふむ。イケてそうだな²。

Go で関数型プログラミング

「配列の全ての要素の最大公約数を求める」で紹介されているコードは高階関数（higher-order function）である reduce() による関数型プログラミングになっている。

Go 言語の関数は第一級関数（first-class function）なので関数型っぽいプログラミングも可能なのだが³， reduce() のような関数は標準では用意されていない。ただし，似たような機能を持つパッケージを公開しておられる人はいる。わざわざ自作するのもナニなので今回は以下のパッケージを利用させてもらおう。

robpike/filter: Simple apply/filter/reduce package.

これを使って先程の例題を以下のコードで解くことができる。

package main

import (
    "fmt"
    "math/big"

    "github.com/robpike/filter"
)

func gcd(m, n uint64) uint64 {
    x := new(big.Int)
    y := new(big.Int)
    z := new(big.Int)
    a := new(big.Int).SetUint64(m)
    b := new(big.Int).SetUint64(n)
    return z.GCD(x, y, a, b).Uint64()
}

func main() {
    values := []uint64{290021904, 927964716, 826824516, 817140688}

    fmt.Println(filter.Reduce(values, gcd, 1).(uint64)) // 92
}

もしくは gcd() 関数自体を引数に組み込んで

package main

import (
    "fmt"
    "math/big"

    "github.com/robpike/filter"
)

func main() {
    values := []uint64{290021904, 927964716, 826824516, 817140688}

    fmt.Println(filter.Reduce(values,
        func(m, n uint64) uint64 {
            x := new(big.Int)
            y := new(big.Int)
            z := new(big.Int)
            a := new(big.Int).SetUint64(m)
            b := new(big.Int).SetUint64(n)
            return z.GCD(x, y, a, b).Uint64()
        },
        1).(uint64)) // 92
}

としてもよい。ほら，これなら「実質的にワンライナー」と呼べないこともない（笑）

robpike/filter パッケージの作者も書いておられるが

I wanted to see how hard it was to implement this sort of thing in Go, with as nice an API as I could manage. It wasn't hard.

Having written it a couple of years ago, I haven't had occasion to use it once. Instead, I just use "for" loops.

You shouldn't use it either.

via robpike/filter

filter.Reduce() 関数を駆動するコストを考えれば⁴ 普通に for 文で回したほうが安上がりだよね。イマドキっぽく関数型言語の利点をいくつか取り込んでいるとはいえ Haskell のようなガッツリした関数型言語とは役割が異なるので，無理に関数型にこだわらなくてもいいということである。

ブックマーク

参考図書

プログラミング言語Go (ADDISON-WESLEY PROFESSIONAL COMPUTING SERIES): Alan A.A. Donovan (著), Brian W. Kernighan (著), 柴田芳樹 (翻訳); 丸善出版 2016-06-20; 単行本（ソフトカバー）; 4621300253 (ASIN), 9784621300251 (EAN), 4621300253 (ISBN), 9784621300251 (ISBN); 評価

著者のひとりは（あの「バイブル」とも呼ばれる）通称 “K&R” の K のほうである。この本は Go 言語の教科書と言ってもいいだろう。

reviewed by Spiegel on 2016-07-13 (powered by PA-APIv5)

改訂2版みんなのGo言語: 松木雅幸 (著), mattn (著), 藤原俊一郎 (著), 中島大一 (著), 上田拓也 (著), 牧大輔 (著), 鈴木健太 (著); 技術評論社 2019-08-01 (Release 2019-08-01); Kindle版; B07VPSXF6N (ASIN); 評価

改訂2版の目玉は7章の「データベースの扱い方」が追加されたことだろう。他の章では，大まかな構成は1版と同じだが細かい部分が変わっていて Go 1.12 への言及まであるのには驚いた。

reviewed by Spiegel on 2019-08-12 (powered by PA-APIv5)

数学ガールの秘密ノート／整数で遊ぼう: 結城浩 (著); SBクリエイティブ 2013-12-17 (Release 2014-07-24); Kindle版; B00L0PDMJ0 (ASIN); 評価

小中学生にお薦め。小学生高学年くらいならギリで理解可能と思われ。

reviewed by Spiegel on 2014-09-26 (powered by PA-APIv5)

数学ガール／フェルマーの最終定理: 結城浩 (著); SBクリエイティブ 2008-07-29 (Release 2014-03-12); Kindle版; B00I8AT1CM (ASIN); 評価

「フェルマーの最終定理」というサブタイトルをみたとき「なんちう大風呂敷を広げるねん」と思ったものだが，実際に読んでみるとぐいぐい引き込まれる。ひっさびさに頭を使ったような気がする。

reviewed by Spiegel on 2019-01-13 (powered by PA-APIv5)

結城浩さんが連載しておられる「数学ガールの秘密ノート」にユークリッドの互除法が出て来る。はやく本にならないかなぁ。 ↩︎
繰り返し処理が1回余分に回っているが $gcd(a, a) = a$ で影響はないのでご容赦。 ↩︎
あくまでも「ぽい」である。たとえば Go 言語では if 文や for 文などは関数でも演算子でもない単なる制御構文（stateement）であり，直接ロジックにコンパイルされる。これまでの手続き型言語と関数型言語の利点を合わせたような言語は「マルチパラダイム・プログラミング言語（multiparadigm programming language）」などと呼ばれたりする。 Python や Swift といった近頃流行りの言語もマルチパラダイムの流れのひとつである。 ↩︎
Go 言語には総称型（Generics）がないため filter.Reduce() 関数内部で reflect パッケージを駆使することになるが，その分はどうしてもパフォーマンスに影響を与えてしまう（参考：きみは Generics がとくいなフレンズなんだね，または「制約は構造を生む」）。しかし reflect パッケージが悪というわけではなく，たとえば先日紹介した sort.Slice() 関数は reflect パッケージを効果的に使用した例といえる。高階関数は見た目はクールだが，それに惑わされることなく目的に適うコードを選ぶことが重要である。とはいえ，勉強のために Go 言語で高階関数を組んでみようというのは悪くないと思う。 ↩︎