サイコロで遊ぶ
Twitter で面白そうな遊びを見つけた。
曰く
有名な統計力学ゲーム。6人が均等にコインを持つとする。サイコロを二つ振り、一つ目の出目の人はコインを中央に、二つ目の出目の人はそのコインを貰う。無い人は出さない(借金なし)。これを繰り返すと少数の金持ちと多数の貧乏人ができる。ルール平等でも貧富の差が。
— Yuki Nagai (@cometscome_phys) 2018年1月8日
早速試してみる。
最初は簡単なルールでやってよう。 準備するものは
- 1から6までの目のサイコロを2つ用意する(サイコロ1,サイコロ2)
- サイコロの出目は完全にランダムとする
- サイコロの目(1から6)に対してそれぞれプレイヤーを割り当てる(合計6人のプレイヤー)
- 所持金は全員0からスタート。所持金の上下限なし(借金OK)
とする。 この状態から以下のプレイを繰り返す。
- 2つのサイコロを同時に振る
- サイコロ1の出目に対応するプレイヤーは所持金から1を差し出す($-1$)
- サイコロ2の出目に対応するプレイヤーは差し出された金額を所持金に加える($+1$)
- その他のプレイヤーは所持金に増減なし
サイコロ1とサイコロ2の出目が同じ場合もあり得るが,その場合は全員増減なしということで。 じゃあこれを Go 言語で書いてみる1。
package main
import (
"fmt"
"math/rand"
"time"
)
//Dices is dice list
type Dices [2]int
//New returns generator of Dices
func New(s rand.Source, max int, count int64) <-chan Dices {
ch := make(chan Dices)
r := rand.New(s)
go func(r *rand.Rand, count int64) {
for i := int64(0); i < count; i++ {
ch <- Dices{r.Intn(max), r.Intn(max)}
}
close(ch)
}(r, count)
return ch
}
func main() {
max := 6
persons := make([]int64, max)
ch := New(rand.NewSource(time.Now().UnixNano()), max, 10)
ct := 1
for d := range ch {
if d[0] != d[1] {
persons[d[0]]--
persons[d[1]]++
}
fmt.Printf("%d\t%d\t%d\t%d\t%d\t%d\t%d\n", ct, persons[0], persons[1], persons[2], persons[3], persons[4], persons[5])
ct++
}
}
雑なコードだけどご容赦を。 これを実行すると以下のようになる。
$ go run main.go
1 1 0 0 -1 0 0
2 1 -1 0 -1 1 0
3 1 -1 0 -1 1 0
4 0 -1 0 -1 1 1
5 0 0 0 -2 1 1
6 -1 1 0 -2 1 1
7 -1 0 0 -2 1 2
8 -1 0 -1 -2 1 3
9 -1 0 0 -2 1 2
10 -1 0 -1 -2 1 3
まぁ10回くらいじゃよく分からないよね。
では試行回数を1万回にしてやってみよう。
実行結果を dice.dat ファイルに格納して
$ go run main.go > dice.dat
gnuplot でグラフ化してみる。 グラフ化のコマンドは以下の通り。
unset key
plot "dice.dat" using 1:2 title "Person 1" with lines,\
"dice.dat" using 1:3 title "Person 2" with lines,\
"dice.dat" using 1:4 title "Person 3" with lines,\
"dice.dat" using 1:5 title "Person 4" with lines,\
"dice.dat" using 1:6 title "Person 5" with lines,\
"dice.dat" using 1:7 title "Person 6" with lines
結果はこんな感じ。

じゃあ今度はどどーんと100万回でやってみようか。 結果はこんな感じ
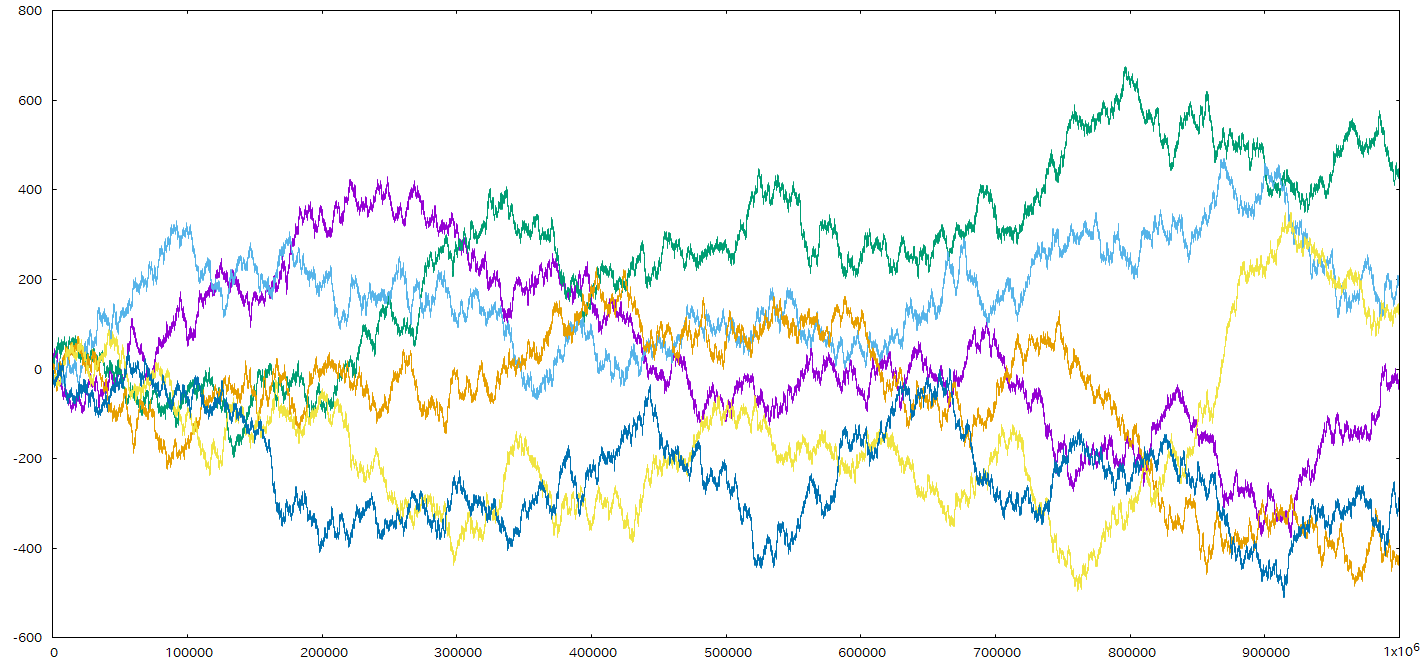
傾向としては「試行を繰り返すほど概ね貧富の差が大きくなる」ことは言えそうだ。
上のグラフでは順位が比較的容易に入れ替わってるように見えるが,実際には100万回のセットを何度か繰り返すと
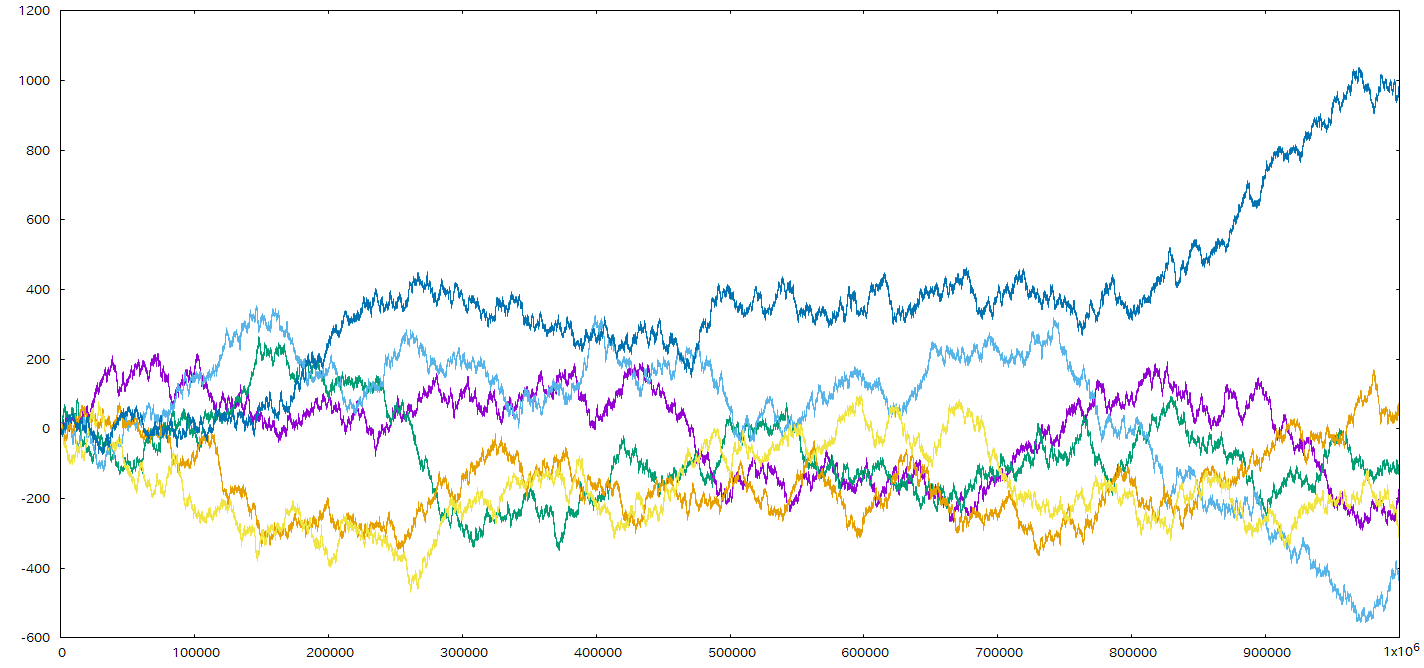
のように上位者が固定してしまうこともあるみたいだ(更に試行回数を増やせば順位も変わるかもしれないが)。
では少しルールを変えて,所持金について
- 所持金は全員100からスタート。所持金は0以上のみ有効(借金NG)
とし,お金を差し出す側が所持金0の場合は取引不成立とする。
これで最初の tweet のルールと同じ。
コードで書くとこんな感じかな(main() 関数のみ)。
func main() {
max := 6
init := int64(100)
persons := []int64{init, init, init, init, init, init}
ch := New(rand.NewSource(time.Now().UnixNano()), max, 1000000)
ct := 1
for d := range ch {
if d[0] != d[1] && persons[d[0]] > 0 {
persons[d[0]]--
persons[d[1]]++
}
fmt.Printf("%d\t%d\t%d\t%d\t%d\t%d\t%d\n", ct, persons[0], persons[1], persons[2], persons[3], persons[4], persons[5])
ct++
}
}
結果は以下のような感じになる。
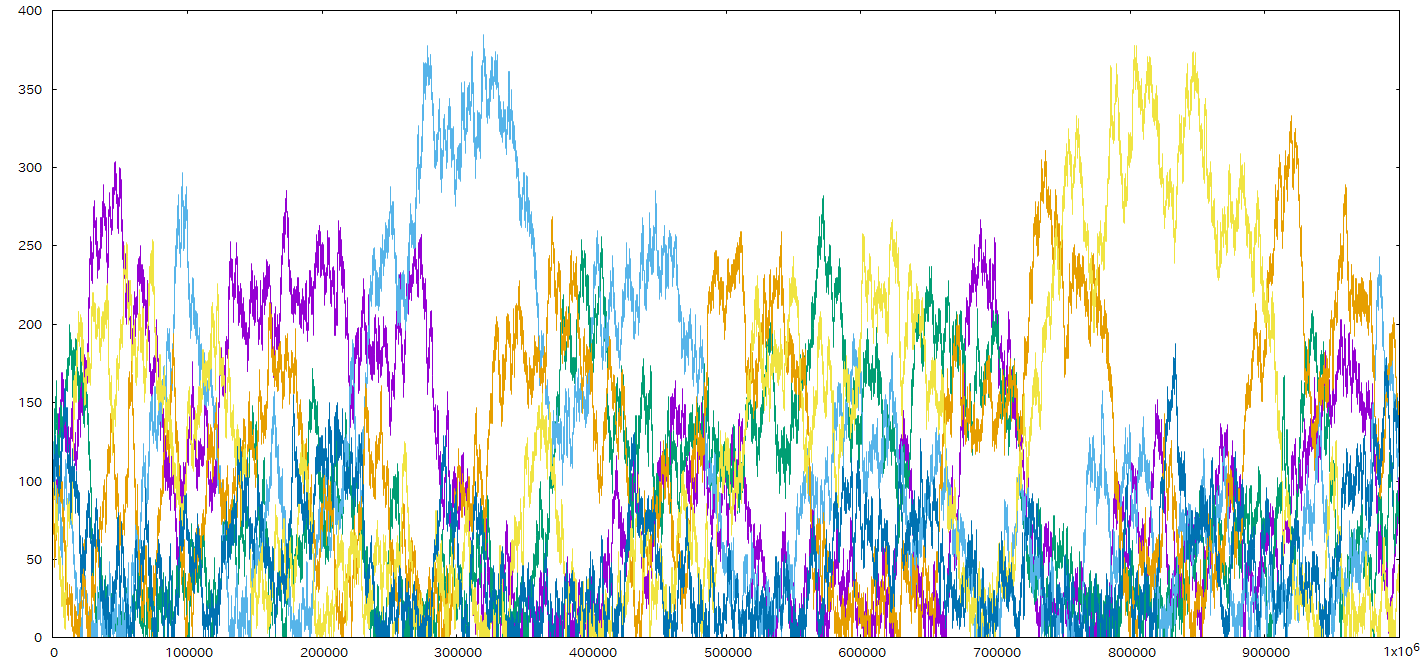
所持金の総量が決まってるので,それ以上貧富の差は広がらない。 その範囲の中で激しく順位が入れ替わってる感じである(激しい順位の入れ替わりは100万回試行を何度繰り返しても現れる)。
さて,これって現実世界に何か教訓めいたことが言えるだろうか… まぁいいか。 お正月だし「双六で楽しく遊びました」ということにしよう(笑)
-
ちなみに Go 言語標準の疑似乱数生成器(非暗号用)のアルゴリズムは「ラグ付フィボナッチ法(Lagged Fibonacci Generator)」と呼ばれるものだそうだ。詳しくは「モンテカルロ法による円周率の推定(その4 PRNG)」を参照のこと。 ↩︎
