モンティ・ホール問題で遊ぶ

有名な数学問題なので知ってる人も多いと思うけど一応解説すると，「モンティ・ホール問題」というのは Monty Hall という人が司会をつとめるアメリカの番組 “Let’s make a deal” 内で行われたゲームに関する問題である。

簡単にルールを紹介する。

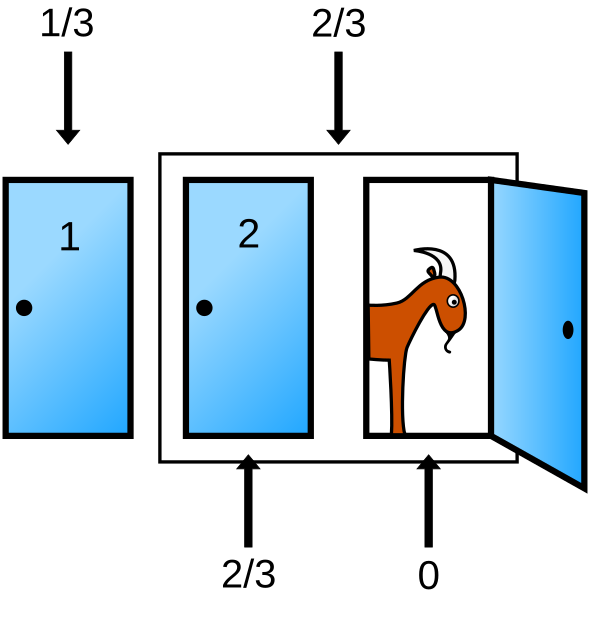
プレイヤーの前に閉まった3つのドアがある。1つのドアの後ろには景品の新車が，2つのドアの後ろには（はずれを意味する）ヤギがいる
プレイヤーが1つのドアを選択
司会者が残りのドアのうちヤギがいるドアを開けてヤギ（＝はずれ）を見せる
プレイヤーは最初に選んだドアを変更してもよい

このときプレイヤーは最初に選択したドアを変更したほうが得（つまり当たる確率が高い）かどうか，というのが「モンティ・ホール問題」のあらましである。

この問題について「ドアを変更したほうが当たる確率が高い」と示した女性がいて，これに対して猛烈な反発が起こり大論争になったらしい（女性蔑視な発言もあったそうで，今なら確実にハラスメント案件だよなw）。

ポイントは3番目の「はずれのドアを開ける」部分で（司会者はどのドアが当たりかあらかじめ知っている），残りの2つのドアのどちらかが当たりなのだからというので多くの人が直感的に「当たる確率は半々」だと思った，博士号保持者も含めて。

この問題は事後確率（posterior probability）と呼ばれるものの一種である¹。最初の選択で当たる確率は $1 / 3$ なので後半に変更しなければ $1 / 3$ のままだが，「はずれのドアを開ける」ことにより選択肢が既に選択したドアともうひとつのドアの2つになるため，ドアを変更した場合の当たる確率が $2 / 3$ （つまり半々より確率値が大きい）になるのである。

「モンティ・ホール問題」は直感と論理との乖離を示す好例として挙げられることが多く，また簡単な確率シミュレーションとしてプログラミングの演習問題に使われることもあるようだ。

というわけで「モンティ・ホール問題」をシミュレートするコードを Go 言語で組んでみよう（Go 言語で書くことに特に意味はない。皆さんはお好きな言語でどうぞ）。

package main

import (
    "fmt"
    "math/rand"
    "time"
)

func selectDoor(limit, max int) <-chan int {
    ch := make(chan int)
    go func() {
        defer close(ch)
        rand.Seed(time.Now().UnixNano())
        for i := 0; i < max; i++ {
            ch <- rand.Intn(limit)
        }
    }()
    return ch
}

func challenges(shuldChange bool, max int) int {
    doors := []bool{true, false, false}
    ch := selectDoor(len(doors), max)
    count := 0
    for n := range ch {
        result := doors[n]
        if shuldChange {
            result = !result
        }
        if result {
            count++
        }
    }
    return count
}

func main() {
    max := 10000
    fmt.Println("nochange:", float64(challenges(false, max))/float64(max))
    fmt.Println("  change:", float64(challenges(true, max))/float64(max))
}

Go 言語的に面白いトピックはないので詳細は省くが，ざっくり説明すると selectDoor() 関数は（疑似乱数を使って）ドアを選択する関数で選択したドアを指定回数だけ channel で返す。 challenges() 関数は「モンティ・ホール問題」を指定回数だけ試行するもので，当たりの回数を返している。ドアを変更するか否かは引数 shuldChange で指定する。変数 doors がプレイヤーが選択するドアで，当たりが true に相当する。 for-range 構文の中身が実際に「モンティ・ホール問題」を試行している部分で

for n := range ch {
    result := doors[n]
    if shuldChange {
        result = !result
    }
    if result {
        count++
    }
}

ドアを変更しない場合はそのまま，変更する場合は真偽が反転する。これは「はずれのドアを開ける」と当たりとはずれのドアが必ずひとつづつになるため，最初に選択したドアとそうでないドアで真偽が反対になるからである。

では実際にコードを実行してみる。

$ go run monty-hall-problem.go
nochange: 0.3464
  change: 0.6675

というわけで，それっぽい値になった。めでたし。

「モンティ・ホール問題」は確かに直感に反するが²，こうやって具体的なコードで記述していくと「何故そうなるのか」が何となく分かってくる。どうせプログラミング教育をやるのならこういう感じでやっていただきたいものである（笑）

おまけ：N個のドアでモンティ・ホール問題

応用として $n$ 個のドアで「モンティ・ホール問題」を検証してみよう。ルールはこんな感じ。

プレイヤーの前に閉まった $n$ 個のドアがある（$n \ge 3$）。当たりのドアは $1$ つ。残り $n-1$ 個ははずれ
プレイヤーが $1$ つのドアを選択
司会者が残りのドアのうち $n-2$ 個のはずれドアを開ける
プレイヤーは最初に選んだドアを変更してもよい

まず先ほどのコードのうち challenges() 関数と main() 関数を以下のように変更する。

func challenges(shuldChange bool, dct, max int) int {
    doors := make([]bool, dct, dct) //initialized by false
    doors[0] = true
    ch := selectDoor(len(doors), max)
    count := 0
    for n := range ch {
        result := doors[n]
        if shuldChange {
            result = !result
        }
        if result {
            count++
        }
    }
    return count
}

func main() {
    dct := 3
    max := 10000
    fmt.Println("nochange:", float64(challenges(false, dct, max))/float64(max))
    fmt.Println("  change:", float64(challenges(true, dct, max))/float64(max))
}

これで最初のコードとまったく同じ機能になる。ここで main() 関数内の dct を 100 にして実行してみる。

$ go run monty-hall-problem.go
nochange: 0.0114
  change: 0.9785

何故こういう値になるか考えてみませう。簡単だよね。

おまけ2：有理数表現

Go 言語では math/big パッケージを使った有理数表現 big.Rat が使える。これを使って main() 関数を書き直すと

func main() {
    dct := 3
    max := 10000
    fmt.Println("nochange:", big.NewRat(int64(challenges(false, dct, max)), int64(max)).FloatString(4))
    fmt.Println("  change:", big.NewRat(int64(challenges(true, dct, max)), int64(max)).FloatString(4))
}

てな感じになる。 math/big パッケージを使うと，計算コストは高くなるが，浮動小数点数型特有の計算誤差を緩和できるメリットがある。まぁ，今回はあんまり関係ないけどね。

おおっ。なんか Go 言語っぽい（笑）

参考図書

プログラマの数学第2版: 結城浩 (著); SBクリエイティブ 2018-01-16 (Release 2018-02-08); Kindle版; B079JLW5YN (ASIN); 評価

タイトル通りプログラマ必読書。第2版では機械学習に関する章が付録に追加された。

reviewed by Spiegel on 2018-03-19 (powered by PA-APIv5)

プログラミング言語Go (ADDISON-WESLEY PROFESSIONAL COMPUTING SERIES): Alan A.A. Donovan (著), Brian W. Kernighan (著), 柴田芳樹 (翻訳); 丸善出版 2016-06-20; 単行本（ソフトカバー）; 4621300253 (ASIN), 9784621300251 (EAN), 4621300253 (ISBN), 9784621300251 (ISBN); 評価

著者のひとりは（あの「バイブル」とも呼ばれる）通称 “K&R” の K のほうである。この本は Go 言語の教科書と言ってもいいだろう。

reviewed by Spiegel on 2016-07-13 (powered by PA-APIv5)

事後確率についての説明は割愛する。ベイズ主義とか頻度主義とかちゃんと説明しようとするととてつもなく面倒臭いので。ただし事前確率とか事後確率とかいったものは統計学（ベイズ統計学）ではよく出てくる話なので，興味のある方は自力でどうぞ。 ↩︎
「モンティ・ホール問題」はジレンマやパラドックスの一種と見なされることがあるらしい。実際には論理的な矛盾はないので疑似パラドックスといったところだろうけど。 ↩︎