モンテカルロ法による円周率の推定(その3 Gaussian)
- モンテカルロ法による円周率の推定(その1)
- モンテカルロ法による円周率の推定(その2 CLI)
- モンテカルロ法による円周率の推定(その3 Gaussian) ← イマココ
- モンテカルロ法による円周率の推定(その4 PRNG)
推定結果の分布
さて,前回書いたコードを利用して,いよいよ円周率の推定結果を評価してみる。
CLI はこんな感じになった。
$ go run main.go estmt --help
Estimate of Pi with Monte Carlo method.
Usage:
pi estmt [flags]
Flags:
-e, --ecount int Count of estimate (default 100)
-p, --pcount int Count of points (default 10000)
Global Flags:
--config string config file (default is $HOME/.pi.yaml)
まずは円周率の推定処理を10,000回繰り返してみる。 また推定処理のためのランダムな点の数 $n$ を1,000個,10,000個,100,000個と変えて実行してみようか。
$ go run main.go estmt -e 10000 -p 1000 > estmt1k.dat
minimum value: 2.94800
maximum value: 3.31600
average value: 3.14199
standard deviation: 0.05104 (69.9%)
$ go run main.go estmt -e 10000 -p 10000 > estmt10k.dat
minimum value: 3.07240
maximum value: 3.20360
average value: 3.14178
standard deviation: 0.01654 (68.0%)
$ go run main.go estmt -e 10000 -p 100000 > estmt100k.dat
minimum value: 3.12360
maximum value: 3.16184
average value: 3.14163
standard deviation: 0.00518 (68.3%)
最後のはさすがに時間がかかるので,お茶でも飲みながら優雅に待ちましょう(笑)
標準エラー出力に最小値,最大値,平均値($E$),標準偏差($\sigma$)を出力してみた。 標準偏差の後ろの括弧は $\left[ E-\sigma, E+\sigma \right]$ の範囲にある推定値の割合を示したものだ。
円周率の推定処理の試行回数が十分大きいなら推定値の分布は正規分布(またはガウス分布)に近似できる筈である。
(以下の図は Wikimedia Commons のものを拝借した。 CC-BY-2.5 Generic で公開されている)
そこで $n=100,000$ のときの推定結果についてヒストグラムを描いてみる。 幸いなことに gnuplot では簡単にヒストグラムを作図できる。 こんな感じ(階級幅を0.001としている)。
gnuplot> filter(x,y)=int(x/y)*y
gnuplot> plot "estmt100k.dat" u (filter($1,0.001)):(1) smooth frequency with boxes lc rgb "black"
gnuplot の出力結果はこんな感じ。
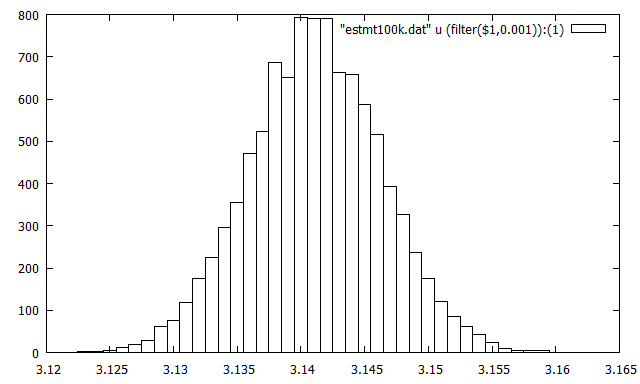
んー。 まぁ正規分布っぽい?
もうひとつ,正規確率の分布を調べてみよう。 これも gnuplot で描こうと思ったけど,少し面倒そうなので,ズルして以下を参考に LibreOffice の Calc で描くことにした1。
とりあえず結果だけ。
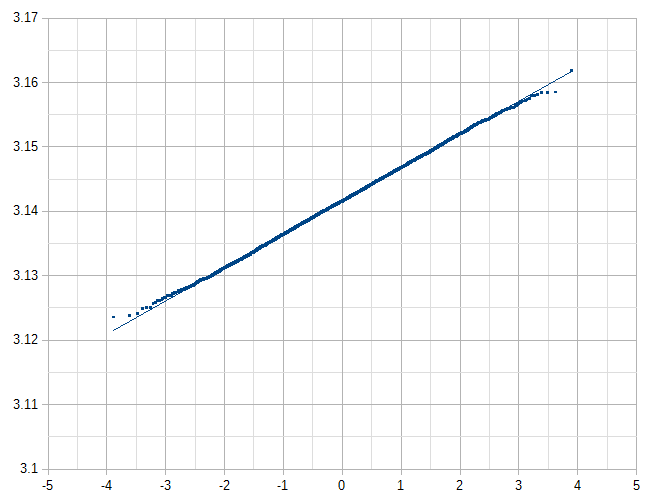
プロットが直線状に並んでいれば正規分布であると言える。 図から見る限り,概ね正規分布になっているようである。
しまった。 ここまで Go 言語が全然出てこなかった。 まぁ,いいや。 多分あと1回続きます。
おまけ:誤差評価
モンテカルロ法を使ってどの程度の精度で円周率が求まるかの考察については以下が参考になる。
これも横着して結果だけを拝借すると, $n=100,000$ で推定を行った場合の値の分布は,中央値を $\pi$,99%信頼区間を $\frac{4.230}{\sqrt{100,000}} = 0.013$ として, $\left[ \pi - 0.013, \pi + 0.013 \right]$ の範囲になるようだ。
おまけの追記: 正規確率の分布図について
正規確率の分布図(Q-Q プロット)を描くのに毎回 Excel や Calc を使うのもどうかという気がしたので,こちらのプログラム側であらかじめ計算して,結果のプロット・データを gnuplot に食わせるよう考えてみる。
まず qq サブコマンドを追加し,この qq サブコマンド時にデータファイルを読み込んで Q-Q プロットの計算を行うように CLI を変更する。(ついでに他のオプションも整理した)
$ go run main.go qq --help
make Q-Q plot data.
Usage:
pi qq [data file] [flags]
Global Flags:
-p, --pcount int Count of points (default 10000)
実際の処理部分はこんな感じ。
//Execute output Q-Q plot data.
func Execute(cxt *Context) error {
scanner := bufio.NewScanner(cxt.ui.Reader())
pis := make([]float64, 0)
for scanner.Scan() {
pi, err := strconv.ParseFloat(scanner.Text(), 64)
if err != nil {
return errors.Wrap(err, "invalid data")
}
pis = append(pis, pi)
}
ecf := float64(len(pis))
sort.Float64s(pis)
for i, pi := range pis {
rank := (float64(i+1) - 0.5) / ecf
cxt.ui.Outputln(fmt.Sprintf("%v\t%v", qnorm(rank), pi))
}
return nil
}
qnorm() 関数は標準正規分布に対する累積分布関数の逆関数の値を返すのだが(Excel の NORM.S.INV 関数相当),Go 言語で書かれた適当なパッケージが見つからなかったので(もしあれば誰か教えて)以下のページのコードを Go 言語用に書き直した。
実際にはこんな感じ2。
//qnorm function refers to http://rangevoting.org/Qnorm.html
// This function is licensed under GNU GPL version 3 or later.
func qnorm(p float64) float64 {
const (
split = 0.42
a0 = 2.50662823884
a1 = -18.61500062529
a2 = 41.39119773534
a3 = -25.44106049637
b1 = -8.47351093090
b2 = 23.08336743743
b3 = -21.06224101826
b4 = 3.13082909833
c0 = -2.78718931138
c1 = -2.29796479134
c2 = 4.85014127135
c3 = 2.32121276858
d1 = 3.54388924762
d2 = 1.63706781897
)
q := p - 0.5
ppnd := float64(0)
if math.Abs(q) <= split {
r := q * q
ppnd = q * (((a3*r+a2)*r+a1)*r + a0) / ((((b4*r+b3)*r+b2)*r+b1)*r + 1)
} else {
r := p
if q > 0 {
r = 1 - p
}
if r > 0 {
r = math.Sqrt(-math.Log(r))
ppnd = (((c3*r+c2)*r+c1)*r + c0) / ((d2*r+d1)*r + 1)
if q < 0 {
ppnd = -ppnd
}
}
}
return ppnd
}
では早速動かしてみよう。
$ go run main.go qq estmt100k.dat > qq100k.dat
生成した qq100k.dat ファイルを gnuplot に食わせる。
こんな感じでいいだろう。
gnuplot> unset key
gnuplot> set style line 1 pointsize 0.1 pointtype 7 linecolor rgb "black"
gnuplot> plot "qq100k.dat" linestyle 1
結果はこんな感じ。

ついでにこの分布図にフィットする直線 $y=ax+b$ の $a, b$ 値を調べてみる。
gnuplot> f(x)=a*x+b
gnuplot> fit f(x) "qq100k.dat" via a,b
iter chisq delta/lim lambda a b
0 5.5761271099e+04 0.00e+00 1.00e+00 1.000000e+00 1.000000e+00
1 6.0252530865e-04 -9.25e+12 1.00e-01 5.277253e-03 3.141418e+00
2 4.5071534394e-05 -1.24e+06 1.00e-02 5.177775e-03 3.141632e+00
3 4.5071534393e-05 -1.23e-06 1.00e-03 5.177775e-03 3.141632e+00
iter chisq delta/lim lambda a b
After 3 iterations the fit converged.
final sum of squares of residuals : 4.50715e-005
rel. change during last iteration : -1.23364e-011
degrees of freedom (FIT_NDF) : 9998
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 6.71421e-005
variance of residuals (reduced chisquare) = WSSR/ndf : 4.50806e-009
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 0.00517777 +/- 6.715e-007 (0.01297%)
b = 3.14163 +/- 6.714e-007 (2.137e-005%)
correlation matrix of the fit parameters:
a b
a 1.000
b 0.000 1.000
ここで $a$ が標準偏差, $b$ が平均値にマッチしている点に注目。 分布図と上の直線を重ねあわせるとこうなる。

んー。 こんなもんかな。
そうそう。
qq サブコマンドは,フィルタとしても機能するので
$ go run main.go estmt -e 100 -p 10000 | go run main.go qq > qq.dat
minimum value: 3.09640
maximum value: 3.18600
average value: 3.14158
standard deviation: 0.01654 (68.0%)
といった感じにパイプでつなぐこともできる。
ブックマーク
- gnuplot でヒストグラム(頻度分布図)を描画する - Qiita
- 【統計学】Q-Qプロットの仕組みをアニメーションで理解する。 - Qiita
- 簡単な例題:最小2乗法でデータに曲線や曲面をあてはめる
- 付表:正規分布表 ( P から z を求める表) - 中川雅央(滋賀大学)
参考図書
- プログラミング言語Go
- アラン・ドノバン (著), ブライアン・カーニハン (著), 柴田芳樹 (著)
- 丸善出版 2016-06-20 (Release 2021-07-13)
- Kindle版
- B099928SJD (ASIN)
- 評価
Kindle 版出た! 一部内容が古びてしまったが,この本は Go 言語の教科書と言ってもいいだろう。感想はこちら。
- 数学ガール/乱択アルゴリズム
- 結城 浩 (著)
- SBクリエイティブ 2011-02-25 (Release 2014-03-12)
- Kindle版
- B00I8AT1FO (ASIN)
- 評価
工学ガール,リサちゃん登場!
- 数学ガールの秘密ノート/やさしい統計
- 結城 浩 (著)
- SBクリエイティブ 2016-10-28 (Release 2016-11-10)
- Kindle版
- B01MSJMKMW (ASIN)
- 評価
統計の本当に基礎の部分から。学業成績でよく聞く「偏差値」とは何を表していて何を意味しているのか。なんてなあたりから。
-
Calc でも Excel の関数がそのまま使えるようだ。助かる。 ↩︎
-
余談だが, Go 言語では untyped な定数を設定できる。型が評価されるのは,処理の中でその定数が使われた時点となる。数値の精度も使用時点で評価されるため,定義では大きい桁数の値を設定しても問題ない。(参考: Go の定数の話 - Qiita) ↩︎


