モンテカルロ法による円周率の推定（その1）
乱数（random number）についていい例題がないかなぁ，と考えて「円周率をモンテカルロ法で求めるやつやればいいぢゃん」と思いついた。 ので早速試してみる。 ちなみに「モンテカルロ法」というのは数値計算やシミュレーションに乱数を用いる手法をさす。
- モンテカルロ法による円周率の推定（その1） ← イマココ
- モンテカルロ法による円周率の推定（その2 CLI）
- モンテカルロ法による円周率の推定（その3 Gaussian）
- モンテカルロ法による円周率の推定（その4 PRNG）
モンテカルロ法による円周率の推定
では乱数を使ってどうやって円周率を求めるのか。 まずは以下のように原点を中心とした半径 $1$ の円を考える。 ただしここでは第一象限のみを対象とする。
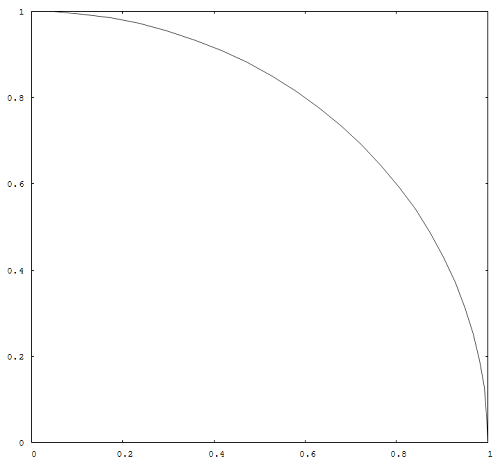
そして $0 \le y \le 1$ および $0 \le y \le 1$ の範囲でランダムに点をプロットしていく。 （以下の図は Wikimedia Commons のものを拝借した。 CC-BY-3.0 で公開されている）
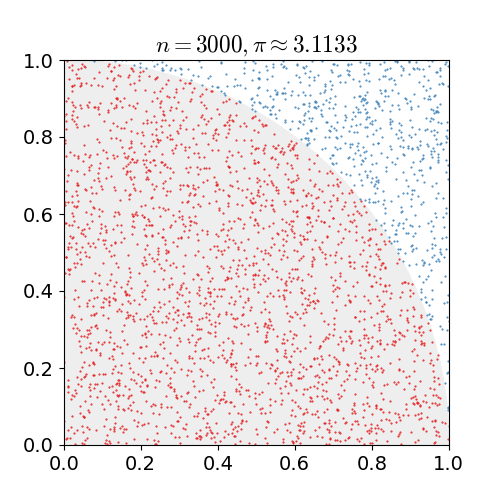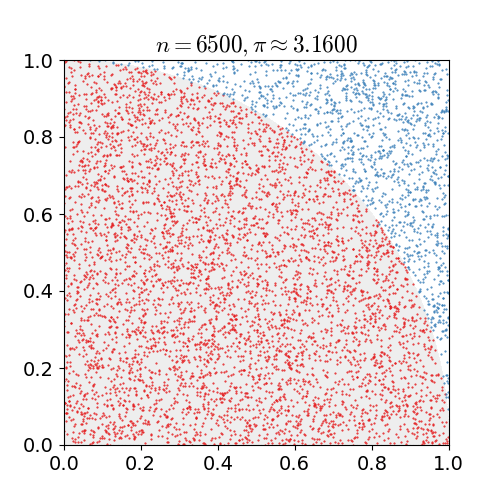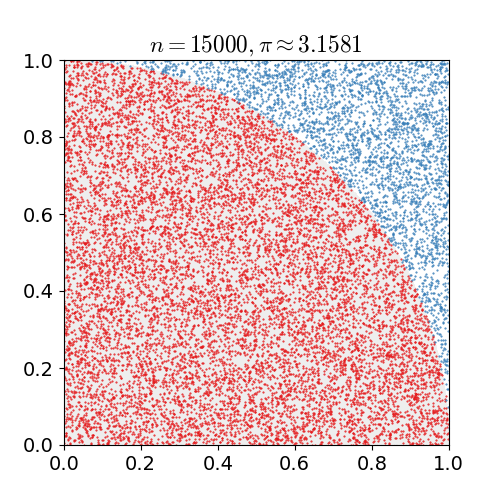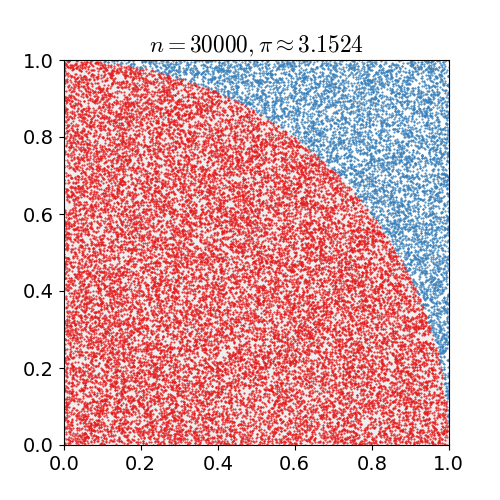
全ての点 $n$ が領域内に均等にプロットされていれば，円の内側に入る点の数 $m$ は，面積比から，以下の式のようになると期待できる。
\[ m \simeq \frac{1}{4}{\pi}n \]
この式を $\pi$ を求める形に変形すると
\[ \pi \simeq \frac{4m}{n} \]
となる。 プロットした点が円の内側かどうかは原点からの距離で判定できる。 すなわち
\[ \sqrt{x^2 + y^2} \le 1 \]
を満たしていればよい。
math/rand パッケージ
Go 言語 にはコア・パッケージとして math/rand が用意されていて，このパッケージを使って擬似乱数を発生させることができる。
今回は $0 \le r \le 1.0$ の範囲で乱数を発生させればいいのだが，生憎そのものズバリな関数が用意されていない。
たとえば rand.Float64() が吐く値の範囲は $0 \le r \lt 1.0$ なのでそのままでは使えないのだ。
そこで，こんなコードを考えてみる。
package main
import (
"fmt"
"math/rand"
"time"
)
func main() {
rand.Seed(time.Now().UnixNano())
for i := 0; i < 10; i++ {
fmt.Println(float64(rand.Int63n(10000001)) / float64(10000000))
}
}
rand.Int63n(n) 関数は $0 \le i \lt n$ の範囲で整数を吐く。
$n=10,000,001$ なら $0 \le i \le 10,000,000$ の範囲になる。
これを $10,000,000$ で割って $0 \le r \le 1.0$ の範囲の乱数を作るのである。
実際には2次元座標なので複素数（complex）表現にして
package main
import (
"fmt"
"math/cmplx"
"math/rand"
"time"
)
func main() {
rand.Seed(time.Now().UnixNano())
for i := 0; i < 10; i++ {
c := complex(float64(rand.Int63n(10000001))/float64(10000000), float64(rand.Int63n(10000001))/float64(10000000))
fmt.Printf("%v (%v)\n", c, cmplx.Abs(c))
}
}
とすればよい。
ちなみに cmplx.Abs() 関数は複素数の絶対値を取るもので， $\sqrt{x^2 + y^2}$ と同じである。
では，以上を踏まえてランダムな点を生成する gencmplx パッケージを作ってみよう。
channel と goroutine を使ってこんな感じにするかな。
package gencmplx
import "math/rand"
//New returns generator of random complex number
func New(s rand.Source, count int64) <-chan complex128 {
ch := make(chan complex128)
r := rand.New(s)
go func(r *rand.Rand, count int64) {
for i := int64(0); i < count; i++ {
ch <- complex(float64(r.Int63n(10000001))/float64(10000000), float64(r.Int63n(10000001))/float64(10000000))
}
close(ch)
}(r, count)
return ch
}
後々のことを考えて，乱数の rand.Source1 と生成する点の個数は引数で指定するようにした。
いっぽう， gencmplx パッケージの呼び出し側はこんな感じになる。
package main
import (
"fmt"
"math/rand"
"time"
"github.com/spiegel-im-spiegel/pi/gencmplx"
)
func main() {
c := gencmplx.New(rand.NewSource(time.Now().UnixNano()), int64(10000))
for p := range c {
fmt.Printf("%v\t%v\n", real(p), imag(p))
}
}
ここでは少なめに1万個の点を生成している。
channel c からの値の取り出しは for-range 構文を使うと記述がシンプルになり c が close() するまでループしてくれる。
早速これを動かしてみよう。
$ go run main.go > plot-1.dat
これで1万個の点を plot-1.dat に格納したことになる。
plot-1.dat を gnuplot に食わせてみるとこんな感じ。
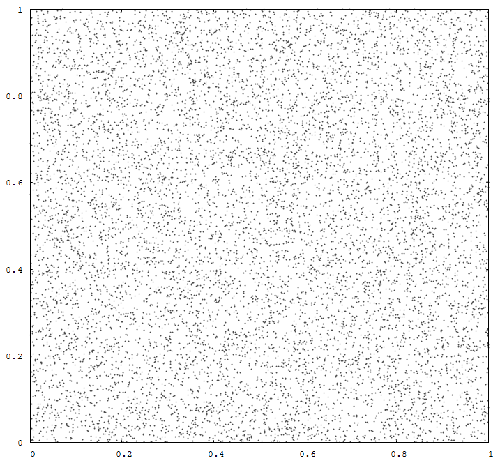
うーん。 均等？ なのかなぁ。 まぁ，この辺の評価については「その3」以降で。
最後に，生成した点の集合から円周率を推定するところまでやってみよう。
main() 関数はこのように変える。
package main
import (
"fmt"
"math/cmplx"
"math/rand"
"time"
"github.com/spiegel-im-spiegel/pi/gencmplx"
)
func main() {
c := gencmplx.New(rand.NewSource(time.Now().UnixNano()), int64(100000))
n := int64(0) // total
m := int64(0) // plot in circle
for p := range c {
n++
if cmplx.Abs(p) <= float64(1) {
m++
}
}
fmt.Printf("n = %v, m = %v, 4m/n = %v\n", n, m, float64(4*m)/float64(n))
}
点の数は10万個まで増やしている。 実行結果は
$ go run main2.go
n = 100000, m = 78397, 4m/n = 3.13588
と，まぁそれっぽい値が出てきた。
今回はここまで。
ブックマーク
参考図書
- プログラミング言語Go (ADDISON-WESLEY PROFESSIONAL COMPUTING SERIES)
- Alan A.A. Donovan (著), Brian W. Kernighan (著), 柴田 芳樹 (翻訳)
- 丸善出版 2016-06-20
- 単行本（ソフトカバー）
- 4621300253 (ASIN), 9784621300251 (EAN), 4621300253 (ISBN), 9784621300251 (ISBN)
- 評価
著者のひとりは（あの「バイブル」とも呼ばれる）通称 “K&R” の K のほうである。この本は Go 言語の教科書と言ってもいいだろう。
- 数学ガール／乱択アルゴリズム
- 結城 浩 (著)
- SBクリエイティブ 2011-02-25 (Release 2014-03-12)
- Kindle版
- B00I8AT1FO (ASIN)
- 評価
工学ガール，リサちゃん登場！