地球が遠日点を通過する話

かねてより「夏至付近ってパッとした天文イベントがないよなぁ」と思っていたが， Bluesky で自 TL を眺めてたときに見つけたこのネタは面白そうだ。

2025年7月4日、地球は太陽から最も遠ざかる「遠日点通過」を迎えます。

「遠日点通過」と太陽に最も近づく「近日点通過」、実は月との関係で、数日単位で動くのだそうです。
eco.mtk.nao.ac.jp/koyomi/wiki/...

実際にどれくらい動くのか調べてみました。
【参考】ほしぞら情報(国立天文台)
www.nao.ac.jp/astro/sky/

2020年7月4日
2021年7月6日
2022年7月4日
2023年7月7日
2024年7月5日
2025年7月4日

二十四節気も、うるう年の関係などで1日前後動きますが、それどころじゃない複雑で大きな動き方をしています。

[image or embed]
— 星が好きな人のための新着情報 (@localgroupjp.bsky.social) June 29, 2025 at 11:37 PM

「星が好きな人のための新着情報」さん，いつもお世話になっています。

とういうわけで今回は，地球公転軌道における近日点と遠日点の話。

2025年の近日点と遠日点通過日は以下の通り。

日付	曜日	内容
2025-01-04	土	地球が近日点通過
2025-07-04	金	地球が遠日点通過

「えー？夏に遠日点を通過するのかよ。しかも冬至や夏至とズレてるし」って思わなかった？私は子どもの頃にそう思った（南半球は冬だけど）。

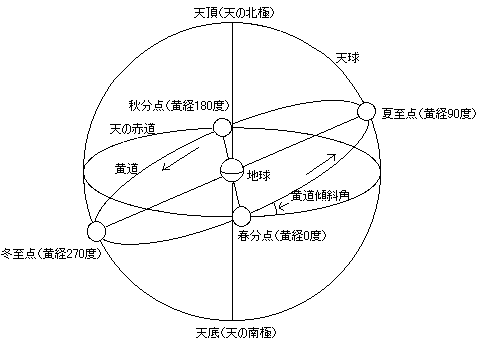
実は冬至や夏至といった二十四節気は、地球の公転面（黄道）に対する自転軸の傾きで決まる。

via Explanation about a celestial sphere in Japanese

一方で近日点と遠日点は地球の公転軌道が関係している。

つまり（ケプラーの法則に基づき）地球の公転軌道を楕円と見立てたときに楕円の焦点にある太陽から最も近づいた瞬間が近日点であり、最も遠ざかった瞬間が遠日点となる。

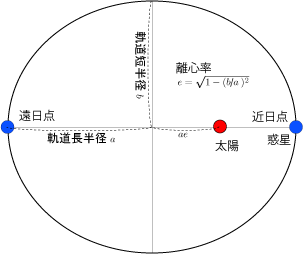
ちなみに，上の図のように軌道長半径を $a$ 軌道短半径を $b$ としたとき，離心率 $e$ は以下で表される¹。

$$ e = \sqrt{1 - \left(\frac{b}{a}\right)^2} $$

離心率 $e$ が $0$ に近いほど円軌道に近くなる²。ちなみに地球公転軌道の離心率は $0.01670$ とされている³。まぁ，ほぼ円やね⁴。

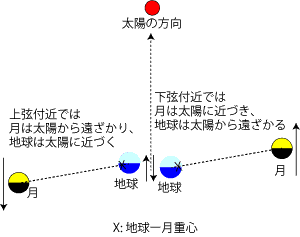
太陽と地球だけを考えれば概ねこれで OK だけど，実際には地球の周りには月が周回している。なので地球-月の間の重心で考える必要がある⁵。これにより太陽-地球-月の位置関係により（地球から見た）近日点および遠日点の通過日が微妙に変わるらしい。

最初に紹介したポストにあるように2020年以降に限っても数日単位で遠日点通過日がシフトしている。

2020年7月4日
2021年7月6日
2022年7月4日
2023年7月7日
2024年7月5日
2025年7月4日

2025年7月4日、地球は太陽から最も遠ざかる「遠日点通過」を迎えます...より

結構激しいな。二十四節気も閏年の関係で1〜2日程度の変動が起きるが，それどころじゃないねぇ。

というわけで，近日点・遠日点の話でした。これで，こっぽし。

ブックマーク

【🌟 星学手簡】江戸時代の天文学者の手紙が重要文化財に！？ VTuberと辿る暦の歴史【星見まどか / 国立天文台】 - YouTube

【🌟 10時間目】江戸時代の天文学🔭望遠鏡や地動説はいつから？【#スクールオブチューブ江戸時代講座 / 星見まどか】 - YouTube

参考

天文年鑑 2025年版: 天文年鑑編集委員会 (編集); 誠文堂新光社 2024-12-05 (Release 2024-12-05); 単行本; 4416723660 (ASIN), 9784416723661 (EAN), 4416723660 (ISBN); 評価

天文ファン必携。2025年版。これが届くと年末って感じ。

reviewed by Spiegel on 2024-12-05 (powered by PA-APIv5)

天体物理学: Arnab Rai Choudhuri (著), 森正樹 (翻訳); 森北出版 2019-05-28; 単行本; 4627275110 (ASIN), 9784627275119 (EAN), 4627275110 (ISBN); 評価

興味本位で買うにはちょっとビビる値段なので図書館で借りて読んでいたが，やっぱり手元に置いておきたいのでエイヤで買った。まえがきによると，この手のタイプの教科書はあまりないらしい。内容は非常に堅実で分かりやすい。理系の学部生レベルなら問題なく読めるかな。

reviewed by Spiegel on 2019-11-13 (powered by PA-APIv5)

暦の大事典: 岡田芳朗 (編集), 神田泰 (編集), 佐藤次高 (編集), 高橋正男 (編集), 古川麒一郎 (編集), 松井吉昭 (編集); 朝倉書店 2014-07-29; 大型本; 4254102372 (ASIN), 9784254102376 (EAN), 4254102372 (ISBN); 評価

古今東西の暦について網羅されている。結構なお値段だが図書館で借りて読んだ。

reviewed by Spiegel on 2016-05-05 (powered by PA-APIv5)

天体の位置計算: 長沢工 (著); 地人書館 1985-09-01; 単行本; 4805202254 (ASIN), 9784805202258 (EAN), 4805202254 (ISBN); 評価

B1950.0 分点から J2000.0 分点への過渡期に書かれた本なので情報が古いものもあるが，基本的な内容は位置天文学の教科書として充分通用する。

reviewed by Spiegel on 2015-01-11 (powered by PA-APIv5)

猫暦(1) (ねこぱんちコミックス): ねこしみず美濃 (著); 少年画報社 2014-10-14 (Release 2016-02-15); Kindle版; B01BHGVLOY (ASIN); 評価

「寛政の改暦」のころの伊能勘解由（忠敬）とその妻とされる「おえい」の物語。感想はこちら。

reviewed by Spiegel on 2016-05-06 (powered by PA-APIv5)

厳密には「軌道離心率」と呼び，幾何学で言う離心率とは異なる。この記事では「離心率」で統一する。 ↩︎
離心率が $0$ で円軌道となり $1$ で放物線軌道となる。さらに $1$ より大きくなると双曲線軌道となる。 ↩︎
ここで挙げた地球公転軌道の離心率は「天文年鑑」2025年版のデータを元にしている。この本によると「2025年1月1日0時 TT の平均軌道要素と，これから得られたもの」とある（年の単位は365.25日，J2000.0の黄道と平均春分点準拠）。ちなみに TT は座標時系のひとつである地球時（Terrestrial Time）を指す。また TAI (International Atomic Time; 国際原子時) も座標時系として再定義されていて $TT = TAI + 32.184\,\mathrm{sec}$ の関係がある。さらに UTC との関係は閏秒の累積を考慮して $TT = UTC + 69.184\,\mathrm{sec}$ (2025年初の時点) である。 ↩︎
有名なハレー彗星は76年周期で回帰するとされているが（次の近日点通過は2061年8月23日頃），離心率は $0.967786$ と見積もられている。2017年に発見された恒星間天体 ‘Oumuamua は離心率が $1$ より大きい双曲線軌道である。 ↩︎
大きなタイムスケールで見れば太陽系の他の天体との相互作用も考慮する必要があるが，この記事では割愛する。 ↩︎